HOME | DD
 FractalMonster — Not from the Mandelbrot Set3
by-nc-sa
FractalMonster — Not from the Mandelbrot Set3
by-nc-sa
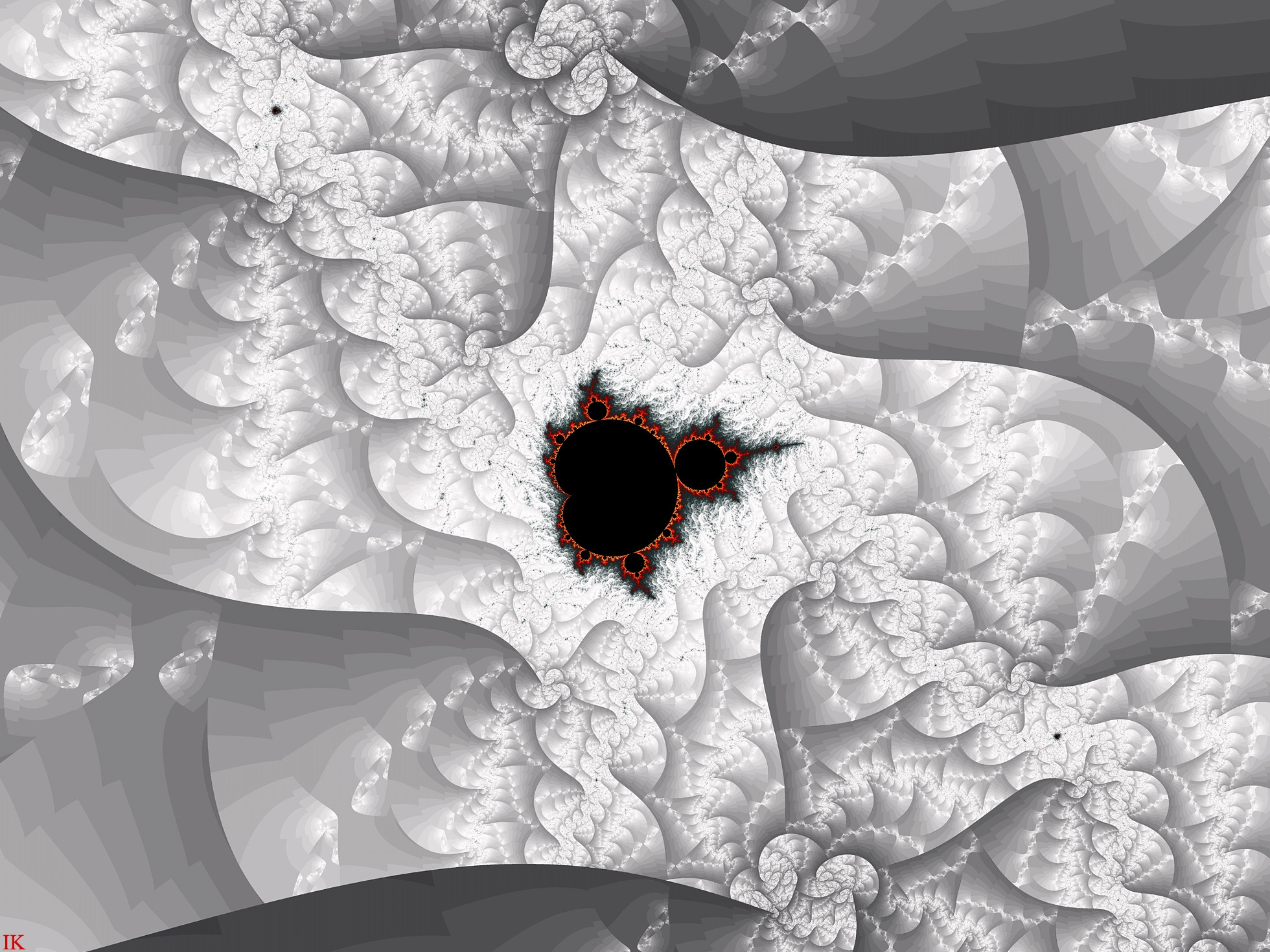
#compass #exponent #formula #play
Published: 2019-04-20 21:37:32 +0000 UTC; Views: 519; Favourites: 20; Downloads: 8
Redirect to original
Description
Here is another tiny mandy I found playing around with the exponent in my compass formula, z -> z^d - da^(d-1) z. See my journal Fractal CompassesNow, my dear readers, I wanna promote the article,27) Compasses
in my Chaotic series. Along with this journal there are four deviations uploaded,
Compass_d=2
Compass_d=3
Compass_d=4
Compass_d=5
The “d” is the exponent in the iterated polynom p(z) = z^d - da^(d-1) z, the a-plane plotted and “z” initialized to the critical point z = +a. Why this formula is called the “Compass formula”? Well, just look at the above deviations, especially for d = 3 and higher






 For d = 3 we actually have z^3 - 3a^2 z whic
For d = 3 we actually have z^3 - 3a^2 z whic 






The exponent "d" in this motive is set to EDIT 0+2i.
Software: Ultra Fractal.
Formula: Extended Compasses (adding a parameter "b". the full parameter space becoming a four dimensional hyper space).
Below the UF parametr file. Play and have fun







NotFromTheMandelbrotSet3 {
fractal:
title="Not from the Mandelbrot Set3" width=800 height=600 layers=1
credits="Ingvar Kullberg;4/13/2019"
layer:
caption="Background" opacity=100 method=multipass
mapping:
center=1.26858565718/0.03192831804955 magn=164.80136
formula:
maxiter=10000 percheck=off filename="ik3.ufm"
entry="ExtendedCompasses" p_exponent=0/2
p_PlottedPlane="1.(a-real,a-imag)" p_hide=yes p_areal=0.0
p_aimag=0.0 p_breal=0.0 p_bimag=0.0 p_xrot=0.0 p_yrot=0.0
p_xrott=0.0 p_yrott=0.0 p_zrot=0.0 p_LocalRot=no p_diff=yes
p_bailout=10000000 p_dbailout=1E-10
inside:
transfer=none
outside:
density=0.1 transfer=linear
gradient:
smooth=yes rotation=-117 index=1 color=1709847 index=13
color=16579582 index=22 color=3026462 index=62 color=223 index=80
color=255 index=-241 color=57075 index=-30 color=16777212
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 4

This has so much more definition than the grey one does; or at least appears that it has more. I love how silky this looks and it changes the appearance of the "depth" of the view. I love it!
👍: 0 ⏩: 1




























